(Unofficial) Assassin 94

[mhparker]

Hi folks,

Looking for something to get that gray matter in motion? Here's something that might do the trick . An attractive but deadly cage pattern that should require a tad more brain power than last week's puzzle, although nothing an experienced Assassin forum member shouldn't be able to handle...


Unofficial Assassin 94 (UA94) (Est. rating: 1.5)



3x3::k:38402818179620533079:41055643:56435134:51345393:4105:5643:5643:5141:5141:5141:5134:5134:5393:4105:5643:6941:69418480:8480:5134:5393:4900:4900:4900:6941848015784397:6958:6941:69418480:8480:64524397:6958:695838976452:645243976958:69586452:6452:46782880186639073661:4678:4678:

Happy weekend!

Cheers,
Mike

P.S. Was hoping to use the new SS 3.0 for the screenshot, but am getting a font rendering problem on my machine. Anyone else having the same problems?

[Caida]

Thanks for the puzzle!

It was just what I needed to help me procrastinate

Below is my walkthrough. I can't remember off-hand how the ratings go - but this didn't "feel" too difficult. I think it's about a 1 (maybe 1.25).

Cheers,

Caida

Unofficial Assassin 94 Walkthrough
Preliminaries:

a. 11(2)n12 = {29/38/47/56} (no 1)
b. 7(2)n2 and n78 = {16/25/34} (no 7..9)
c. 20(3)n2 = {389/479/569/578} (no 1,2)
d. 8(2)n23 = {17/26/35} (no 4,8,9)
e. 21(3)n36 = {489/579/678} (no 1..3)
f. 19(3)n4 = {289/379/469/478/568} (no 1)
g. 9(3)n5 = {126/135/234} (no 7..9)
h. 33(5)n56 = {36789/45789} (no 1,2)
i. 6(3)n6 = {123} (no 4..9)
i1. -> 1,2,3 locked for n6 and r5 -> no 1,2,3 elsewhere in n6 and r5
j. 10(3)n69 = {127/136/145/235} (no 8,9)
j1. -> r78c9 no 6,7
k. 11(3)n7 = {128/137/146/236/245} (no 9)
l. 15(2)n8 = {69/78} (no 1..5)
m. 14(2)n89 = {59/68} (no 1..4,7)



1. 9(3)n5:
1a. -> r46c5 = {12/13/23} (no 4,5,6)

2. Innies c5: r37c5 = 14(2) = {59} -> locked for c5
Note: combo {68} blocked by 15(2)n8
2a. -> 15(2)n8 = {78} -> locked for n8 and c5
2b. -> r9c7 no 6
2c. -> r12c5 no 2
2d. -> 2 in c5 locked in n5 -> no 2 elsewhere in n5

3. 15(3)n8 = [159/195/591/951/294/492/456/654] (no 3)
3a. -> 9 in n8 is locked in 15(3)n8 and r9c6 -> no 9 elsewhere in n8

4. 19(3)n4 = {478/568} -> no 9
4a. -> 8 locked for n4 and r5
4b. -> killer pair {46} in r5 in 19(3)n4 and r5c5 -> no 4,6 elsewhere in r5

5. Outies r1: r2c258 = 8(3) = {125/134} (no 6..9)
5a. -> 1 locked for r2
5b. -> r1c5 no 1

6. Outies r9: r8c258 = 20(3) = [389/479/578/587/785/875]
6a. -> r8c2 no 1,2,6
6b. -> r8c8 no 1,2,3,4,6

7. Innies c1234: r37c4 = 8(2) = [35/62/71]
7a. -> r3c4 no 4,5,8,9
7b. -> r7c4 no 4,6,9

8. 20(3)n2 = [398/794/659/695/758]
8a. -> r3c6 no 3,6,7

9. 15(3)n8 = [159/195/591/294]
9a. -> r7c6 no 2,6

10. Innies c6789: r37c6 = 13(2) = [49/85/94]
10a. -> r3c6 no 5
10b. -> r7c6 no 1
10c. -> r7c4 no 5 (step 9)
10d. -> r3c4 no 3 (step 7)

11. Innies r5: r5c456 = 20(3) = {479/569}
11a. -> 9 locked for r5 and n5 -> no 9 elsewhere in r5 or n5
Note: I could have just said that 9 in r5 was locked in n5 -> no 9 elsewhere in n5 (but I liked finding the h20(3) – and I wind up using this later on)

12. 11(3)n7: r9c12 no 8

13. r5c4 no 7 -> here’s how:
13a. -> if r5c4 = 7 -> r5c456 = [749](step 11) -> r3c4 = 6 -> 20(3)n2 = [659] this puts a 9 in both r35c4

14. 15(3)n8 does not equal [195] -> here’s how:
14a. -> if 15(3)n8 = [195] -> 20(3)n2 = [758] (steps 2,7,10) -> 14(2)n89 = [68](r9c6 must be 6 as {59} are used in 15(3)n8) -> this eliminates all 8s from 33(5)n56 -> no combo possible for 33(5)
14b. -> 15(3)n8 does not equal [159] -> here’s how:
14c. -. If 15(3)n8 = [159] -> 20(3)n2 = [794] (steps 2,7,10) -> r1c6 = 1 -> this eliminates all possible combos for 7(2)n2
14d. -> 15(3)n8 = [294]
14e. -> 20(3)n2 = [659] (step 2,7,10)
14f. -> 7(2)n2 = {34} -> locked for n2 and c5
14g. single: r5c5 = 6
14h. -> r5c456 = [965] (step 11)
14i. single: r9c6 = 6
14j. r9c7 = 8
14k. r89c5 = [87]
14l. hidden single: r1c6 = 1
14m. r1c7 = 7
14n. 11(2)n12 = [38]

15. 7(2)n78 = [25]
15a. 11(3)n7 = [7]{13}
15b. 18(3)n9 = [5]{49}
15c. pair {56} locked in r46c3 for c3 and n4
15d. single: r7c3 = 8
15e. hidden single: r3c3 = 1, r2c8 = 1
15f. -> r2c2 = 4 (step 5)

singles and cage sums to the end

[Afmob]

Thanks Mike for providing another interesting Killer. It'll be interesting to see if other users can solve it without resorting to the one difficult move.

But this one move was quite interesting because:

Step 5a) 8,9 is locked in 33(5) = 789{36/45} + Innies C6789 = 13(2) = {49/58} + R9C7 = (89) for C67

The interesting thing is a 8/9 in Innies C6789 forces a 8/9 for R46C7 @ 33(5).
So the Innies do not only effect C6 but also C7 and thereby 14(2) @ R9.
But this also means that the Killer pairs of 14(2) are not only effective for R9 but for C6 too (because 8,9 only possible @ R9C7).

Step 5b) Therefore the Killer pair (58) of 14(2) blocks {58} of Innies in C6.

UA Walkthrough 94:

1. C5
a) Innies = 14(2) = {59} locked since (68) is a Killer pair of 15(2)
b) 7(2) = {16/34}
c) 15(2) = {78} locked for N8
d) 15(3) = {159/249/456} <> 3
e) 9(3) = 2{16/34} -> 2 locked for N5

2. R5+C46
a) 6(3) = {123} locked for R5+N6
b) Innies C6789 = 13(2) = [49/76/85/94]
c) 19(3) = 8{47/56} because R5C5 = (46) blocks {469} -> 8 locked for R5+N4
d) 9 locked in Innies R5 = 20(3) = 9{47/56} -> 9 locked for N5; R5C46 <> 4,6
e) 9(3) must have 4 xor 6 and R5C5 = (46) -> R46C5 <> 4,6
f) Innies C1234 = 8(2) = [35/62/71]
g) 20(3): R3C9 <> 7 because 4,8 only possible there
h) Innies C6789 = 13(2): R7C6 <> 6
i) 15(3) = 9{15/24} -> 9 locked for R7+N8; R7C4 <> 5
j) Innies C1234 = 8(2) = [62/17]

3. R1
a) Outies R1 = 8(3) = 1{25/34} -> 1 locked for R2
b) 7(2): R1C5 <> 1

4. R789
a) Outies R9 = 20(3) = {389/479/578} because R8C5 = (78)
b) Outies R9 = 20(3): R8C8 <> 3,4 because 9 only possible there
c) 10(3): R78C9 <> 6,7 because R6C9 >= 4
d) 9 locked in R8C13 for R8
e) 14(2) = [59/68]
f) Outies R9 = {578} locked for R8
g) 11(3): R9C12 <> 5,6,7,8 because R8C2 = (578)

5. C67 !
a) 8,9 locked in Innies C6789 + 33(5) + R9C7 for C67
b) ! Innies C6789 <> [58] since it's a Killer pair of 14(2):
If Innies = [58] then 33(5) must have 8 @ R46C7 (step 5a)
c) Innies C6789 = {49} locked for C6
d) 33(5) = 789{36/45} -> 9 locked for C7
e) 14(2) = [68] -> R9C6 = 6, R9C7 = 8

6. R789
a) Killer pair (23) locked in 11(3) + 7(2) for R9
b) 18(3) = {459} -> R8C8 = 5, {49} locked for R9+N9
c) 15(2) = [87] -> R8C5 = 8, R9C5 = 7
d) 11(3) = {137} -> R8C2 = 7, {13} locked for R9+N7

7. C6789
a) 21(3) = 7{59/68} because R9C9 = (49) blocks {489} -> 7 locked for C9
b) 10(3) = 3{16/25} because 4,5 only possible @ R6C9 -> 3 locked for C9+N9
c) 4 locked in Innies C9 = 4{19/28}; R1C9 <> 1,2
d) 20(3) = 9{47/56} -> 9 locked for R3+N2
e) 12(3): R12C8 <> 8,9 because R1C9 >= 4
f) 9 locked in R12C9 for C9
g) 18(3) = {459} -> R9C9 = 4, R9C8 = 9
h) 25(5) = {13678} -> R6C8 = 8, R8C6 = 3
i) 2 locked in 10(3) @ N9 = {235} -> R6C9 = 5, R7C9 = 3, R8C9 = 2
j) Hidden Single: R1C6 = 1 @ C6 -> R1C7 = 7

8. N23
a) 7(2) = {34} locked for C5+N2
b) 20(3) = {569} -> R3C4 = 6, R3C5 = 5, R3C6 = 9
c) 11(2) = [38/92]
d) R3C9 = 8, R1C9 = 9
e) 12(3) = {129} -> R1C8 = 2, R2C8 = 1
f) 20(5) = {23456} -> R2C6 = 2, R2C7 = 5, R4C8 = 6, {34} locked for R3
g) R1C3 = 3, R1C4 = 8, R2C4 = 7

9. N17
a) 15(3) = {456} locked
b) Hidden Single: R3C1 = 7 @ N1
c) 16(3) = [871] -> R2C1 = 8, R4C1 = 1
d) 22(5) = {12379} -> R2C3 = 9, R4C2 = 3
e) 17(3) = {269} locked for C1

10. Rest is singles.

Rating: 1.25. This is a one-trick pony and I think this one move Caida and I used is too difficult/advanced for a 1.0 Killer.

[Andrew]

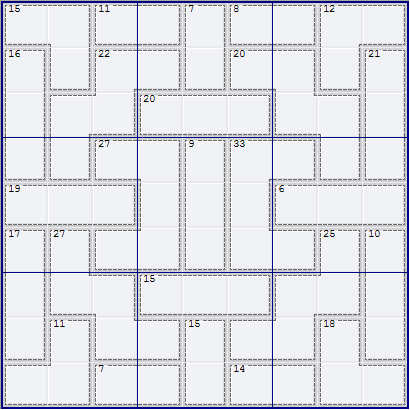
An attractive but deadly cage pattern that should require a tad more brain power than last week's puzzle, although nothing an experienced Assassin forum member shouldn't be able to handle...

Wow, this was a tough one! It stretched my brain power to the limit.

The start was easy, then I ground to a halt and went off to solve YAK94 and then uA95 before I came back and found the key contradiction move. Afmob presents it (steps 5a and 5b) as a clash/block but I felt it is really a short contradiction move (my step 25a). Maybe be source of my difficulty is that the killer pair (my step 23e) mask the fact that they are also used as part of a contradiction move. Very clever Mike!

Between solving YAK94 and uA95 I had another look at this from the start and found a couple of interesting combined cages, particularly the one in step 14; the other one in step 16 didn't really lead anywhere but I've kept it in for completeness.

There are so many possible sets of 4 outies but I only found a couple of them were useful; the one on N3 was the better of the two while the one on R123 gave me a hidden single later.

If I had to rate this puzzle, then it's a 1.25 just on the moves but if difficuly in finding the key breakthrough is taken into account then IMHO it's a 1.5. Clearly Caida, Afmob and Ed (off-forum) thought otherwise since they found breakthrough combination moves much more easily.

Here is my walkthrough

Prelims

a) R1C34 = {29/38/47/56}, no 1
b) R12C5 = {16/25/34}, no 7,8,9
c) R1C67 = {17/26/35}, no 4,8,9
d) R89C5 = {{69/78}
e) R9C34 = {16/25/34}, no 7,8,9
f) R9C67 = {59/68}
g) R3C456 = {389/479/569/578}, no1,2
h) R234C9 = {489/579/678}, no 1,2,3
i) R456C5 = {126/135/234}
j) R5C123 = {289/379/469/478/568}, no 1
k) R5C789 = {123}, locked for R5 and N6
l) R678C9 = {127/136/145/235}, no 8,9
m) 11(3) cage in N7 = {128/137/146/236/245}, no 9
n) 33(5) cage at R4C6 = {36789/45789}, no 1,2

1. R456C5 = {126/135/234}
1a. R5C5 = {456} -> no 4,5,6 in R46C5

2. R678C9 = {127/136/145/235}
2a. 6,7 of {127/136} must be in R6C9 -> no 6,7 in R78C9

3. 45 rule on R1 3 outies R2C258 = 8 = 1{25/34}, 1 locked for R2, clean-up: no 1 in R1C5

4. 45 rule on R9 3 outies R8C258 = 20 = {389/479/569/578}, no 1,2

5. 45 rule on C1234 2 innies R37C4 = 8 = {35}/[62/71]

6. 45 rule on C6789 2 innies R37C6 = 13 = {49/58/67}, no 1,2,3

7. 45 rule on C5 2 innies R37C5 = 14 = {59} (cannot be {68} which clashes with R89C5), locked for C5, clean-up : no 2 in R12C5, no 6 in R89C5

8. Naked pair {78} in R89C5, locked for N8, clean-up: no 5,6 in R3C6 (step 6), no 6 in R9C7
8a. 2 in C5 locked in R46C5, locked for N5

9. R8C258 (step 4) = {389/479/578} (cannot be {569} because R8C5 only contains 7,8), no 6
9a. 9 of {389/479} must be in R8C8 -> no 3,4 in R8C8

10. R3C456 = {389/479/569/578}
10a. 4,8 of {479/578} must be in R3C6 -> no 7 in R3C6, clean-up: no 6 in R7C6 (step 6)
10b. 6 of {569} must be in R3C4, 5 of {578} must be in R3C5 -> no 5 in R3C4, clean-up: no 3 in R7C4 (step 5)

11. R7C456 = {159/249}, 9 locked for R7 and N8, clean-up: no 5 in R9C7
11a. 1,2 only in R7C4 -> R7C4 = {12}, clean-up: no 3 in R3C4 (step 5)

12. 9 in R9 locked in R9C789, locked for N9
12a. R8C258 (step 9) = {578} (only remaining combination), locked for R8

13. 11(3) cage in N7 = {128/137/245} (cannot be {146/236} because R8C2 only contains 5,7,8), no 6
13a. R8C2 = {578} -> no 5,7,8 in R9C12

14. Combined cage 11(3) in N7 + R9C34 = 18(1+4) = 5{1246}/7{1235}/8{1234} (cannot be 5{1346} which isn’t consistent with 11(3) cage), 1,2 locked for R9

15. 18(3) cage in N9 = {378/459/468/567} (cannot be {369} because R8C8 only contains 5,7,8)
15a. 5 of {459} must be in R8C8, 5 of {567} must be in R8C8 (cannot be 7{56} which clashes with R9C6) -> no 5 in R9C89

16. Combined cage 18(3) in N9 + R9C67 = 32(1+4) and must contain 9 (step 12) = 5{4689/5679}/7{3589}/8{3579/3678} (cannot be 8{4569} which clashes with 5{1246} in combined cage 11(3) in N7 + R9C34, other combinations for R9C6789 aren’t consistent with 18(3) cage)
16a. -> 18(3) cage in N9 = {378/459/567} (cannot be {468} which doesn’t fit in combined cage)

17. 45 rule on R5 3 innies R5C456 = 20 = {479/569} (cannot be {578} because R5C5 only contains 4,6), no 8, 9 locked for R5 and N5
17a. R5C5 = {46} -> no 4,6 in R5C46
17b. 8 in R5 locked in R5C123, locked for N4

18. 45 rule on C1 3 innies R159C1 = 12 = {138/147/156/237/246/345} (cannot be {129} because no 1,2,9 in R5C1), no 9
18a. 8 of {138} must be in R5C1 -> no 8 in R1C1

19. 45 rule in C9 3 innies R159C9 = 14 = {149/167/239/248/257/356} (cannot be {158/347} which clash with R234C9)
19a. 1 of {149/167} must be in R5C9 -> no 1 in R1C9

20. 45 rule on R123 4 outies R4C1289 = 17, min R4C89 = 9 -> max R4C12 = 8, no 9

21. 45 rule on N3 4 outies R12C6 + R4C89 = 16, min R4C89 = 9 -> max R12C6 = 7, no 7,8,9, no 6 in R1C6, clean-up: no 1,2 in R1C7

22. 7 in C6 locked in R456C6, locked for N5 and 33(5) cage -> no 7 in R46C7

23. R3C456 (step 10) = {479/569/578}
23a. Hidden killer pair 8,9 in R12C4 and R3C456 for N2 -> R12C4 must contain one of 8,9
23b. Hidden killer pair 8,9 in R12C4 and R456C4 for C4 -> R456C4 must contain one of 8,9
23c. Hidden killer pair 8,9 in R456C4 and R456C6 for N5 -> R456C6 must contain one of 8,9
23d. Hidden killer pair 8,9 in R456C6 and R46C7 for 33(5) cage -> R46C7 must contain one of 8,9
23e. Killer pair 8,9 in R46C7 and R9C7, locked for C7
[A slightly shorter version starts with hidden killer pair 8,9 in R37C6 and R456C6.]

24. 33(5) cage at R4C6 = {36789/45789}
24a. 7 in C6 locked in R456C6 (step 22)
24b. R456C6 must contain one of 8,9 (step 23c) -> only one of 3,4,5,6 is in R456C6
24c. 3 of {36789} must be in R46C6 -> no 6 in R46C6

25. R456C6 and R46C7 must each contain one of 8,9 (steps 23c and 23d)
25a. If R46C7 contains 8 => R9C67 = [59], R5C6 = 9, R37C6 = [85] clashes with R9C6
25b. -> no 8 in R46C7, 9 locked in R46C7, locked for C7, N6 and 33(5) cage -> R9C7 = 8, R9C6 = 6, R89C5 = [87], clean-up: no 1 in R9C34

26. 9 in C6 locked in R37C6 (step 6) = {49}, locked for C6
26a. 8 in C6 locked in R46C6, locked for N5
26b. R5C4 = 9 (hidden single in N5), clean-up: no 2 in R1C3
26c. R4C7 = 9 (hidden single in R4)
26d. 9 in N2 locked in R3C56, locked for R3

27. R234C9 = {489/579/678}
27a. 9 of {489/579} must be in R2C9 -> no 4,5 in R2C9

28. 1 in R9 locked in R9C12, locked for N7
28a. 11(3) cage in N7 (step 13) = {137} (only remaining combination) -> R8C2 = 7, R9C12 = {13}, locked for R9 and N7, R8C8 = 5, clean-up: no 4 in R9C34
28b. Naked pair {49} in R9C89, locked for N9

29. Naked triple {123} in R578C9, locked for C9
29a. R678C9 = {127/136/235} (cannot be {145} because 4,5 only in R6C9), no 4

30. Killer pair 2,5 in R7C456 and R9C4, locked for N8
30a. 2 in N8 locked in R79C4, locked for C4, clean-up: no 9 in R1C3

31. 6,7 in N9 locked in R7C78 + R8C7, locked for 25(5) cage -> no 6,7 in R6C8
31a. 25(5) cage at R6C8 = {13678} (only remaining combination), no 2,4 -> R6C8 = 8
31b. R4C6 = 8 (hidden single in R4)

32. 2 in N9 locked in R78C9, locked for C9
32a. R678C9 (step 29a) = {127/235}, no 6

33. 12(3) cage in N3 = {129/138/147/237/246}
33a. 9 of {129} must be in R1C9 -> no 9 in R1C8

34. R9C8 = 9 (hidden single in C8), R9C9 = 4

35. R234C9 = {579/678}, 7 locked for C9 -> R6C9 = 5
35a. R234C9 = {678}, locked for C9 -> R1C9 = 9, R12C8 (step 33) = {12}, locked for C8 and N3 -> R5C8 = 3, R5C79 = [21]

36. Naked pair {23} in R78C9, locked for N9 -> R8C6 = 3 (step 31a), R56C6 = [57], R12C6 = [12], R1C7 = 7, R12C8 = [21], R6C7 = 4 (step 24), R78C9 = [32], clean-up: no 4 in R1C34, no 6 in R1C5

37. Naked pair {16} in R78C7, locked for C7 and N9 -> R7C8 = 7, R4C89 = [67], R3C8 = 4, R3C6 = 9, R3C5 = 5, R3C4 = 6 (step 23), R23C7 = [53], R23C9 = [68], R7C56 = [94], R78C4 = [21], R46C4 = [43], R12C4 = [87], R1C3 = 3, R12C5 = [43], R2C2 = 4, R5C5 = 6, R78C7 = [16], R9C34 = [25], R3C23 = [21], R3C1 = 7, R46C3 [56], R7C3 = 8, R2C13 = [89], R8C13 = [94], R5C123 = [487], R4C2 = 3, R9C12 = [31], R6C2 = 9

38. R8C1 = 9 -> R67C1 = 8 = [26]

and the rest is naked singles

5 6 3 8 4 1 7 2 9
8 4 9 7 3 2 5 1 6
7 2 1 6 5 9 3 4 8
1 3 5 4 2 8 9 6 7
4 8 7 9 6 5 2 3 1
2 9 6 3 1 7 4 8 5
6 5 8 2 9 4 1 7 3
9 7 4 1 8 3 6 5 2
3 1 2 5 7 6 8 9 4