SudoCue Users

Here is the promised alternative version:



3x3::k4353:4353:4353:5124:4613:4613:4613:461635845124:5124:51244616:4616:4370:43702827:5124385513055148:5148:5148:69432592387530996943:6943:6943:5674387523493366:6943:5674:567418445175:5175:5175:6202261949263126:4673:6202:6202:62024926:49261608:4673:4673:62023141:3663

Enjoy,
Ruud

Below is my walkthrough (again it is how I solved it - so a bit messy in parts)
edited for clarifications and corrections - thanks Andrew!

I didn't find this any harder than the original version - so I would put it as a 1.25 also.

Interested to hear what other thoughts are.

Cheers,

Caida


Assassin 84 v2.38 walkthrough

Preliminaries:

a. 17(2)n1 = {89} -> locked for n1 and r3
b. 5(2)n3 = {14/23} (no 5..7)
c. 9(2)n4 = {18/27/36/45} (no 9)
d. 20(3)n45 and n78 = {389/479/569/578} (no 1,2)
e. 10(3)n56 and n89 = {127/136/145/235} (no 8,9)
f. 7(2)n6 = {16/25/34} (no 7..9)
g. 22(3)n56 = {589/679} (no 1..4)
h. 6(2)n7 = {15/24} (no 3,6..9)
i. 14(2)n9 = {59/68} (no 1..4,7)
j. 19(3)n9 = {379/469/478} (no 1,2,5)
Note combos {289/568} blocked by 14(2)n9
k. killer pair {89} locked for n9 in 19(3)n9 and 14(2)n9 -> no 8,9 elsewhere in n9


1. Outies n1: r13c4 = 14(2) = [85/96]
1a. -> r1c4 no 1..7
1b. -> r3c4 no 1..4, 7
1c. 11(3)n12 = {14/23}[6]/{24}[5]
1d. -> r23c3 no 5,6,7
1e. r1c678 no 1 (combo {189} blocked by r1c4)

2. Outies n3: r13c6 = 11(2) = [47/92]
Note: combo {56} blocked by r3c4
Note: combo [83] blocked by 5(2)n3, 18(3)n23 and 15(3)n23 -> 5(2) would equal {14}, 18(3)n23 would equal [8]{37} -> no possible combination for 15(3)n23
Note: combo [74] blocked by 5(2)n3, 18(3)n23 and 15(3)n23 -> 5(2) would equal {23}, 18(3)n23 would equal [7]{56} -> no possible combination for 15(3)n23
2a. -> r1c6 no 2,3,5,6,7,8
2b. -> r3c6 no 1,3,4,5,6
2c . 18(3)n23 = [4]{59/68}/[9]{27/36}
2d. -> r1c78 no 4
2e. killer pair {89} in r1 in r1c4 and 18(3)n23 -> no 8,9 elsewhere in r1
2f. r2c89 no 1 (no 8,9 in r1c9)
2g. 15(3)n23 = [2]{58}/[7{26/35}
2h. -> r23c7 no 1,4,7,9
2i. -> 5(2)n3 = {14} -> locked for n3 and r3
Note: combo {23} blocked by 15(3)n23
2k. -> r2c3 no 1 (step 1c)
2l. -> 2 locked 11(3)n12 r23c3 -> no 2 elsewhere in n1 and c3

3. Outies n4: r46c4 = 9(2) = {36/45}/[72/81]
3a. -> r4c4 no 9
3b. -> r6c4 no 7,8,9

4. Outies n6: r46c6 = 9(2) = [18/36/45]
Note combo [27] blocked by r3c6
4a. -> r4c6 no 2,5,6,7
4b. -> r6c6 no 7,9
4c. 9 locked in 22(3) within n6 -> locked for n6 and c7
4d. r56c7 no 6

5. Outies n7: r79c4 = 11(2) = {38/47}/[92]
Note: combo {56} blocked by r3c4
5a. -> r7c4 no 5,6
5b. -> r9c4 no 1,5,6,9

6. Outies n9: r79c6 = 10(2) = {37/46}/[18/29] (no 5)
6a. -> r9c6 no 1,2

7. Innies c1234: r258c4 = 11(3) = {128/137/146/236/245} (no 9)

8. Innies c12: r147c2 = 20(3) = {479/569/578} (no 1,2,3)
Note: combo {389} blocked by r3c2
9a. killer pair {89} in c2 in h20(3) and r3c2 -> no 8,9 elsewhere in c2
9b. -> r6c1 no 1

10. 17(3)n12 = [719/539/458/548]
Note: combo [638] blocked by h14(2)n2 (step 1) and 11(3)n12 (if 17(3)n12 = [638] -> r3c4 = 6 (step 1) -> no option available for 11(3)n12))
10a. -> r1c2 no 6
10b. -> r1c3 no 6,7
10c. 14(3)n1 = {167/356} (no 4)
10d. 18(3)n23: r1c78 no 5,9 (combo [4]{59} blocked by 17(3)n12)
10e. 9 locked in n3 in r2 -> no 9 elsewhere in r2
10f. 18(3)n3 = {279/369} (no 5,8)
10g. 5 locked in n3 in c7 -> no 5 elsewhere in c7
10h. 15(3)n23 = [2]{58}/[7]{35}
10i. -> r23c7 no 2,6
10j. r6c6 no 8
10k. -> r4c6 no 1
10l. -> r4c78 no 4,7

11. 4 in c7 locked in n9 -> no 4 elsewhere in n9
11a. -> 19(3)n9 = {379} -> locked for n9
11b. -> 14(2)n9 = {68} -> locked for n9 and r9
11c. hidden single: r7c8 = 5
11d. triple {124} locked for c7

12. r7c67 = {14}/[32]
12a. -> r7c6 no 2,6,7
12b. -> r9c6 no 3,4
a bit circular here – but this is how I saw it
12c. -> r7c6 no 4; r7c7 no 1

13. 10(3)n56 = [361] (only possible combination
13a. 10(3)n89 = [145]
13b. r6c6 = 6
13c. r9c6 = 9
13d. r3c89 = [41]
13e. r1c6 = 4
13f. r3c6 = 7
13g. r56c7 = {79} -> locked for c7 and n6
13h. r23c7 = {35} -> locked for c7 and n3
13i. 18(3)n23 = [486]

14. r1c4 = 9
14a. r3c4 = 5
14b. r23c3 = [42]
14c. singles: r3c7 = 3; r2c7 = 5; r3c5 = 6; r9c89 = [86]; r8c4 = 6 (hidden)
14d. r46c4 no 4
14e. r6c12 no 3
14f. pair {23} locked for n6 and c8 in r56c8
14g. r9c4 no 2,7; r7c4 no 3

15. 18(3)n78 = [873]
Note only other combo left is [954] which is blocked by 6(2)n7


Singles and cage sums to finish

Hi folks,

Was just about to post my rushed WT, only to see that Caida has just beaten me to it! Guess I'll review my WT now before posting (if at all). BTW, I think it's slightly harder than the V1, so I would rate it as 1.5.

P.S. I suspect, in making a point of the "2.38" (which BTW is now 2.75 w/ the latest SS version (2.2.0) w/ default solver settings!), Ruud was hinting that the SScore is too high.

P.P.S. Let's just call it the A84V2...

Hi again folks,

I wrote:Guess I'll review my WT now before posting (if at all).

I've now briefly compared my WT with Caida's. They are quite similar, so I won't provide a full WT, but instead just the following solving outline, simply to show how I got into the puzzle. Note that the key breakthrough move is step 7:

Partial WT for Assassin 84V2

1. 17(2) at R3C12 = {89}, locked for R3 and N3

2. Outies N1: R13C4 = 14(2) = [86/95]

3. Outies N3: R13C6 = 11(2) = [47/74/83/92]
(Note: {56} combo blocked by R3C4)

4. R1C4 blocks {189} combo for 18(3) at R1C6
4a. -> no 1 in R1C78

5. {15689} unavailable in R3C6
5a. -> {159/168} combos blocked for 15(3) at R2C7
5a. -> no 1 in R23C7

6. Innies R1: R1C159 = 10(3)
6a. -> no 8,9
6b. -> 18(3) at R1C6 must have 1 of {89} ({567} blocked)
(Note: alternatively, {567} blocked by 17(3) at R1C2, which requires at least 1 of {567})

7. 18(3) at R1C9 cannot be {189}. Here's how:
7a. 18(3) at R1C9 = {189} forces {8/9} of 18(3) at R1C6 (step 6b) into R1C6
7b. -> R3C6 = {2/3} (step 3)
7c. but this eliminates all combinations for 5(2) at R3C8
7d. Conclusion: 18(3) at R1C9 <> {189}
7e. -> no 1 in 18(3) at R1C9

8. 1 of N3 now locked in R3C89 = {14}, locked for R3 and N3

The rest of the puzzle is fairly straightforward now (nothing worth writing home about).

The use of the chain in step 7 (although fairly quick to spot) was the reason for my rating of 1.5 for this puzzle.

After solving the puzzle, I ran it through JSudoku, which didn't seem to have much trouble with it (compared to some V2s we've had in the past). Interested to see how it did it, I analyzed the log. Here's what I found out:

The key move that JSudoku applied, which avoided the use of chains (but in exactly the same part of the grid as my chain in step 7) was based on the permutational analysis of the hidden innie/outie difference cage at R1C78+R3C6 (see step 4 below). From the candidate diagram shown, JSudoku progressed as follows:

1. 15(3) at R2C7 = {258/267/357/456} = {(5/6)..}
(Note: {348} blocked by 5(2) at R3C8; other combos blocked because both of {19} unavailable)
1a. {56} unavailable in R3C6
1b. -> R23C7 must contain at least 1 of {56}

2. 18(3) at R1C9 = {189/279/369/378/459/468} = {(8/9)..}
(Note: {567} blocked by R23C7 (step 1b))

3. Innies N3: R1C78+R23C7 = 22(4) = {2569/2578/3568/4567}
(Note: {2389} blocked by 18(3) (step 2); {2479/3469/3478} all blocked by 5(2) at R3C8; other combos blocked because 1 unavailable)
3a. 5 locked for N3

4. no 5 in R1C8. Here's how:
4a. I/O diff. N3: R1C78 = R3C6 + 7
4b. -> only possible permutations of R1C78+R3C6 with 5 in R1C8 are:
[452] - blocked by 5(2) at R3C8 = {(2/4)..}
[654] - blocked by R23C7 (step 1)
(Note: {56} blocked for R1C78 anyway, because 18(3) at R1C6 <> {567}, but JSudoku is clearly limiting its analysis to the cells belonging to the I/O diff. cage, and is not also pulling in R1C6 here)
4c. Conclusion: no 5 in R1C8

This locks the 5 of N3 into C7 (-> not elsewhere in C7), which makes a big difference.

Note: Step 4 is an advanced move that would be enough to justify a 1.5 rating on its own, IMHO.

Candidate diagram for JSudoku analysis above:
Hope you found that interesting. I certainly did!

I used the same breakthrough move (step 7 in Mike's walkthrough or step 4f in my WT) as Mike though in a different way by using a forcing chain instead of a contradiction chain.

Edit: Made a combo elimination too soon. Thanks Andrew!

A84 V2 Walkthrough:

1. C123
a) 17(2) = {89} locked for R3+N1
b) Outies N1 = 14(2) = [86/95]
c) 11(3): R23C3 <> 5,6,7 because R3C4 = (56)
d) Outies N4 = 9(2) <> 9 and R6C4 <> 7,8
e) Outies N7 = 11(2): R9C4 <> 1,9
f) Innies N7 = 27(4) = 9{378/468/567} -> 9 locked for N7
g) Innies C12 = 20(3) <> 1,2
h) 14(3) <> 4 because {347} is blocked by Killer pair (34) of 11(3)

2. C1234
a) Innies C12 = 20(3) <> 3 because {389} blocked by R3C2 = (89)
b) Killer pair (89) locked in Innies C12 + R3C2 for C2
c) 9(2): R6C1 <> 1
d) 17(3): R1C3 <> 6,7 because R1C24 >= 12
e) Innies = 11(3) <> 9
f) Outies N7 = 11(2) <> 5,6 because {56} blocked by R3C4 = (56)

3. C789
a) Innies N9 = 12(4) = 12{36/45} -> 1,2 locked for N9
b) 7 locked in 19(3) = 7{39/48}
c) Outies N9 = 10(2) <> 5; R9C6 <> 1,2
d) Outies N6 = 9(2) = [18/27/36/45]
e) 22(3) = 9{58/67} -> 9 locked for C7+N6
f) Outies N3 = 11(2): R1C6 <> 1,2,3; R3C6 <> 1
g) 15(3) @ N3: R2C7 <> 1 because R3C67 <= 13

4. R123 !
a) Innies R1 = 10(3) <> 8,9
b) 18(3) @ R1C6 must have 8 xor 9 because 17(3) can't have both -> 18(3) <> 1
c) 18(3) @ R1C9: R2C89 <> 1 because R1C9 <> 8,9
d) Outies N3 = 11(2) <> 5,6 because it's blocked by R3C4 = (56)
e) 15(3) <> 1 because R3C6 <> 6,8
f) ! Consider combos of 5(2) -> 18(3) @ R1C9 <> 1,4
- i) 5(2) = {14} -> 18(3) @ R1C9 <> 1,4
- ii) 5(2) = {23} -> 15(3) = {456} with R3C6 = 4 and R23C7 = {56} -> 18(3) @ R1C9 <> 4
and R1C6 = 7 (step 3f) -> 18(3) @ R1C6 must have 8 xor 9 @ R1C78 -> 18(3) @ R1C9 <> 1
g) 1 locked in 5(2) = {14} locked for R3+N3
h) 18(3) @ R1C9 <> 5 because {567} blocked by Killer pair (56) of 15(3)
i) 11(3) = 2{36/45} because R3C3 = (23) -> 2 locked for C3+N1
j) 14(3) = 6{17/35} -> 6 locked for N1

5. N23
a) 18(3) @ R1C6 <> 5 because {459} blocked by Killer pair {59} of 17(3)
b) 5 locked in 15(3) = 5{28/37} for C7
c) Outies N3 = 11(2): R1C6 <> 7
d) 6 locked in R3C45 for N2
e) 18(3) @ R1C6: R1C8 <> 9 because R1C6 <> 2,3,6,7
f) 9 locked in 18(3) @ R1C9 = 9{27/36} for R2

6. N69 !
a) 22(3): R6C6 <> 8 because R56C7 <> 5
b) Outies N6 = 9(2): R4C6 <> 1
c) ! 10(3) @ N6: R4C78 <> 4 because R4C6 <> 1,5
d) 4 locked in R789C7 for N9
e) 19(3) = {379} locked for N9
f) 14(2) = {68} locked for R9+N9
g) Hidden Single: R7C8 = 5 @ N9
h) 12(3) must have 7 xor 9 and it's only possible @ R9C6 -> R9C6 = (79)
i) Outies N9 = 10(2) = [19/37]
j) 12(3) = 1{29/47} -> 1 locked for C7
k) 2 locked in R789C7 for C7

7. R789
a) 20(3) = 9{38/47} -> 9 locked for R7
b) Killer pair (34) locked in 20(3)+10(3) for R7
c) Innies R7 = 15(3) = {267} -> R7C9 = 7, {26} locked for R7
d) 10(3) = {145} -> R7C6 = 1, R7C7 = 4
e) Outies N9 = 10(2) = [19] -> R9C6 = 9
f) Outies N7 = 11(2) = {38} -> R9C4 = 3, R7C4 = 8
g) 18(3) = {378} -> R9C3 = 7, R8C3 = 8
h) 20(3) = {389} -> R7C2 = 9, R7C3 = 3

8. N46
a) 13(3) = {256} -> R6C4 = 2, {56} locked for C4+N6
b) Outies N4 = 9(2) = {27} -> R4C4 = 7
c) 9(2) = {18} -> R6C1 = 8, R6C2 = 1
d) 7(2) = {34} locked for R6+N6
e) 10(3) = {136} -> R4C6 = 3, R4C7 = 6, R4C8 = 1
f) Outies N6 = 9(2) = {36} -> R6C6 = 6

9. Rest is singles.

Rating: Easy 1.5. Without using the forcing chain this assassin would have required lots of combo crunching.

Thanks Ruud for a really challenging variant.

Afmob wrote:Without using the forcing chain this assassin would have required lots of combo crunching.

Prompted by that comment I tried to solve it without using a chain but gave up after step 22 where I had reached almost the same diagram as in Mike's 2nd message. I felt that my step 23 was a shortcut but maybe it doesn't count as a shortcut if one can't find any other way forward.

Mike's JSudoku analysis from his diagram is very interesting; I must admit I hadn't thought of looking at that particular relationship. It also works from the position after my step 22 except for the last line which doesn't yet apply. I wonder how much more work would be required to make that apply without resorting to the use of any chains.

I'll rate A84V2 as 1.5 using the contradiction chain. I wonder what the rating would be without using it? I wouldn't be surprised if SS rated it much higher since it will probably look at heavy combo crunching before trying any contradiction or forcing chain.

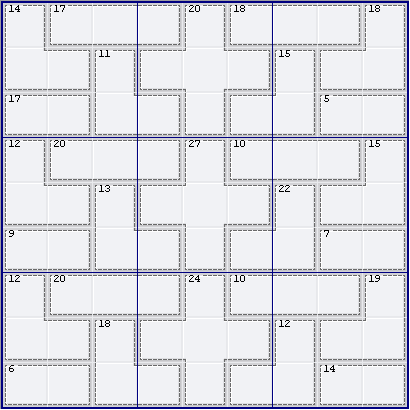
Here is my walkthrough for A84V2

Prelims

a) R3C12 = {89}, locked for R3 and N1
b) R3C89 = {14/23}
c) R6C12 = {18/27/36/45}, no 9
d) R6C89 = {16/25/34}, no 7,8,9
e) R9C12 = {12/45}
f) R9C89 = {59/68}
g) R4C234 = {389/479/569/578}, no 1,2
h) R4C678 = {127/136/145/235}, no 8,9
i) 22(3) cage at R5C7 = 9{58/67}
j) R7C234 = {389/479/569/578}, no 1,2
k) R7C678 = {127/136/145/235}, no 8,9
l) 19(3) cage in N9 = {289/379/469/478/568}, no 1

1. 45 rule on R1 3 innies R1C159 = 10 = {127/136/145/235}, no 8,9

2. 45 rule on N1 2 outies R13C4 = 14 = [86/95]

3. 45 rule on N3 2 outies R13C6 = 11 = {47}/[83/92] (cannot be {56} which clashes with R3C4), no 1,5,6, no 2,3 in R1C6

4. 45 rule on N4 2 outies R46C4 = 9 = {36/45}/[72/81], no 9, no 7,8 in R6C4

5. 45 rule on N6 2 outies R46C6 = 9 = [18/27/36/45], no 9, no 5,6,7 in R4C6

6. 45 rule on N7 2 outies R79C4 = 11 = {38/47}/[92] (cannot be {56} which clashes with R3C4), no 1,5,6, no 9 in R9C6

7. 45 rule on N9 2 outies R79C6 = 10 = [19/28]/{37/46}, no 5, no 1,2 in R9C6

8. 9 in 22(3) cage locked in R56C7, locked for C7 and N6

9. Hidden killer pair 8,9 in R1C4 and R1C678 -> R1C678 must contain 8/9 but not both = {279/369/378/459/468} (cannot be {189/567}), no 1

10. 18(3) cage at R1C9 = {189/279/369/378/459/468/567}
10a. 8,9 only in R2C89 -> no 1 in R2C89

11. 12(3) cage in N7 = {138/156/237/246} (cannot be {129/147/345) which clash with R9C12), no 9
11a. Killer pair 1,2 in 12(3) cage and R9C12, locked for N7

12. 19(3) cage in N9 = {379/469/478/568} (cannot be {289} which clashes with R9C89), no 2
12a. Killer pair 8,9 in 19(3) cage and R9C89, locked for N9
[I missed the clash of {568} with R9C89; fortunately the 19(3) cage was further reduced in step 16.]

13. 11(3) cage at R2C3 = {146/236/245} (cannot be {137} because R3C4 only contains 5,6}, no 7
13a. R3C4 = {56} -> R23C3 = {14/23/24}, no 5,6

14. 15(3) cage at R2C7 = {258/267/357/456} (cannot be {159/168} because R3C7 only contains 2,3,4,7, cannot be {348} because R3C67 = {34} clashes with R3C389), no 1
14a. 4 of {456} must be in R3C6 -> no 4 in R23C7

15. 45 rule on N9 4 innies R7C78 + R89C7 = 12 = {1236/1245}, no 7
15a. R7C78 cannot be {26} (because R7C678 cannot be 2{26}) and cannot be {35} which clashes with R7C78 + R89C7 -> no 2 in R7C6, clean-up: no 8 in R9C6 (step 7)

16. 7 in N9 locked in 19(3) cage = {379/478}, no 5,6
[Alternatively killer pair 5,6 in R7C78 + R89C7 and R9C89, locked for N9.]

17. 45 rule on C12 3 innies R147C2 = 20 = {479/569/578} (cannot be {389} which clashes with R3C2), no 1,2,3
17a. Killer pair 8,9 in R147C2 and R3C23, locked for C2, clean-up: no 1 in R6C1

18. 45 rule on C1234 3 innies R258C4 = 11 = {128/137/146/236/245}, no 9

19. Min R1C24 = 12 -> max R1C3 = 5

20. R23C3 = {14/23/24} (step 13a)
20a. 14(3) cage in N1 = {167/257/356} (cannot be {347} which clashes with R23C3), no 4

21. 4 in N1 locked in R1C23 + R23C3
21a. 45 rule on N1 4 innies R1C23 + R23C3 = 14 = {1247/1346/2345}

22. 45 rule on N3 4 innies R1C78 + R23C7 = {2389/2569/2578/3568/4567} (cannot be {2479/3469/3478} which clash with R3C89)
22a. 18(3) cage at R1C9 (step 10) = {189/279/369/378/567} (cannot be {459/468} which clash with R1C78 + R23C7), no 4

[At this stage I have reached Mike’s candidate diagram except that he has eliminated 5 from the 18(3) cage in N3 (Mike's diagram has since been edited to add those 5s and his analysis changed to allow for them) and I have eliminated an extra pair from R79C6 with step 15a. It looks extremely difficult to find a way forward using combo crunching so I tried a contradiction move.]

23. 18(3) cage at R1C9 (step 22a) = {189/279/369/378/567}
23a. If {189} => R3C89 = {23}, R1C6 = {89} (step 9 with no 8,9 in R1C78) => R3C6 = {23} (step 3) clashes with R3C89
23b. -> 18(3) cage = {279/369/378/567}, no 1

24. 1 in N3 locked in R3C89 = {14}, locked for R3 and N3, clean-up: no 7 in R1C6 (step 3)

25. 11(3) cage at R2C3 (step 13) = {236/245} (cannot be {146} because R3C3 only contains 2,3), no 1, 2 locked in R23C3 for C3 and N1

26. 14(3) cage in N1 (step 20a) = {167/356}, 6 locked for N1

27. R1C678 (step 9) = {279/369/378/459/468}
27a. 5 of {459} must be in R1C7 -> no 5 in R1C8
27b. 18(3) cage at R1C9 (step 23b) = {279/369/378} (cannot be {567} which clashes with R1C78), no 5

28. 5 in N3 locked in R123C7, locked for C7, clean-up: no 8 in R6C6, no 1 in R4C6 (step 5), no 4 in R7C8 (step 15)
28a. R1C78 + R23C7 = {2569/2578/3568}
28b. Only valid permutations are R1C78 = {27/36/59/68} and R23C7 = {26/35/58}
28c. -> no 8 in R1C6, no 7 in R23C7, no 3 in R3C6 (step 3)
28d. 7 in R3 locked in R3C56, locked for N2

29. 12(3) cage at R8C7 = {129/147/237/246}
29a. 7 of {237} must be in R9C6 -> no 3 in R9C6, clean-up: no 7 in R7C6 (step 7)

30. R1C159 (step 1) = {127/136/235} (cannot be {145} because no 1,4,5 in R1C9), no 4

31. R4C678 = {127/136/145/235}
31a. 4 of {145} must be in R4C6 -> no 4 in R4C78
31b. 2,3 of {127/136/235} must be in R4C6 -> no 2,3 in R4C78
31c. 4 in C7 locked in R789C7, locked for N9

32. Hidden killer pair 2,3 in 15(3) cage and R6C89 for N6, neither can have both 2 and 3 -> 15(3) cage and R6C89 must each have one of 2,3
32a. R6C89 = {25/34}, no 1,6
32b. 15(3) cage = {258/267/348} (cannot be {357} which clashes with R6C89), no 1
32c. 1 in N6 locked in R4C78, locked for R4
32d. R6C12 = {27/36}/[81] (cannot be {45} which clashes with R6C89), no 4,5

33. R7C678 = {136/145/235}
33a. 5 of {235} must be in R7C8 -> no 2 in R7C8
33b. 2 in N9 locked in R789C7, locked for C7

34. 19(3) cage in N9 = {379} (only remaining combination), locked for N9, clean-up: no 5 in R9C89
34a. Naked pair {68} in R9C89, locked for R9 and N9, clean-up: no 4 in R7C6 (step 7)
34b. Naked triple {124} in R789C7, locked for C7 and N9 -> R7C8 = 5, clean-up: no 2 in R6C9
34c. R7C67 = 5 = [14/32], no 6 in R7C6, no 1 in R7C7, clean-up: no 4 in R9C6 (step 7)

35. R4C8 = 1 (hidden single in R4), R4C67 = 9 = [37/46], no 2, R3C89 = [41], clean-up: no 7 in R6C6 (step 5), no 6 in R56C7, no 3 in R6C9

36. 3 in C7 locked in R123C7, locked for N3
36a. 18(3) cage at R1C9 = {279} (only remaining combination), locked for N3, 9 locked in R2C89 for R2
36b. Naked pair {68} in R19C8, locked for C8

37. R1C78 + R23C7 (step 28a) = {3568} (only remaining permutation)
37a. Only valid permutations (step 28b) are R1C78 = {36/68}, no 5 and R23C7 = {35/58}, no 6
37b. 6 locked in R1C78, locked for R1
37c. 6 in N1 locked in R2C12, locked for R2

38. R7C234 = {389/479}, no 6, 9 locked for R7
38a. Killer pair 3,4 in R7C234 and R7C67, locked for R7 -> R7C9 = 7, R12C9 = [29], R2C8 = 7, R8C89 = [93], clean-up: no 4 in R7C234 (step 38)

39. Naked triple {389} in R7C234, locked for R7 -> R7C67 = [14] (step 34c), R9C6 = 9 (step 7), R1C6 = 4, R3C6 = 7 (step 3)
39a. R1C78 = {68} (step 27), locked for R1 and N3 -> R1C4 = 9, R3C4 = 5 (step 2), R23C7 = [53], R3C3 = 2, R2C3 = 4 (step 25), R3C5 = 6, R7C15 = [62], R4C6 = 3, R6C6 = 6 (step 5), R4C7 = 6 (step 31), R1C78 = [86], R9C89 = [86], clean-up: no 4 in R46C4 (step 4), no 3 in R6C12, no 3 in R7C4, no 4,7 in R9C4 (both step 6)
39b. R79C4 = [83], R7C23 = [93], R3C12 = [98], R8C6 = 5, R4C4 = 7, R6C4 = 2 (step 4), R6C89 = [34], R5C8 = 2, R5C6 = 8, R2C6 = 2, R45C9 = [85], R2C4 = 1, R12C5 = [38], R2C12 = [36], R58C4 = [46]

40. R4C1 = 2 (hidden single in R4), R5C12 = 10 = [73], R56C7 = [97], R5C35 = [61], R6C12 = [81], clean-up: no 5 in R9C1, no 4 in R9C2

and the rest is hidden and naked singles and a cage sum

5 7 1 9 3 4 8 6 2
3 6 4 1 8 2 5 7 9
9 8 2 5 6 7 3 4 1
2 4 9 7 5 3 6 1 8
7 3 6 4 1 8 9 2 5
8 1 5 2 9 6 7 3 4
6 9 3 8 2 1 4 5 7
4 2 8 6 7 5 1 9 3
1 5 7 3 4 9 2 8 6

Andrew wrote:Thanks Ruud for a really challenging variant.

Yes indeed, thanks Ruud! In particular, the difficulty of the puzzle was well-judged. Hard enough to require a bit of human ingenuity, yet not so hard that we were forced to resort to T&E.

Andrew wrote:I felt that my step 23 was a shortcut but maybe it doesn't count as a shortcut if one can't find any other way forward.

It's interesting to note that you found essentially the same chain as I did (step 7 of my partial WT). It's a perfectly valid chain in that none of the links depend on the side-effects (i.e., candidate/combo eliminations) of any preceding links, which is one of my main criteria for determining whether or not a chain is T&E. However, it's quite a complicated chain. If it were to be expressed in a formalized fashion, my step 7 would look something like this:

Select text in box (e.g., by triple-clicking it) to see what I wrote:(1)r3c89=(1,89)r1c9+r2c89-(8/9)r1c78=(8/9)r1c6,(2/3)r3c6-(23=1)r3c89

Note: I'm using the notation: "xy" => "x AND y", "x/y" => "x OR y" and "A,B" => "premise A => premise B (neutral link)". Note also that the chain begins with a strong link, as is the convention for AICs.

In other words:

7. Either r3c89 contains a 1, OR...
7a. r3c89 does not contain a 1
7b. -> r1c9+r2c89 must contain a 1 (strong link, N3)
7c. -> r1c9+r2c89 must also contain both 8 and 9 (neutral link, 18(3)n3)
7d. -> r1c78 cannot contain an 8 or 9 (weak link, N3)
7e. -> r1c6 must contain an 8 or 9 (strong link, 18(3)n23)
7f. -> r3c6 must contain a 2 or 3 (neutral link, h11(2)r13c6)
7g. -> r3c89 cannot contain both a 2 and a 3 (weak link, R3)
7h. -> r3c89 must contain a 1 (strong link, 5(2) cage)
7i. Conclusion: r3c89 must contain a 1

Suddenly, the chain looks a lot more complex! However, it's important to note that just because I often express chains in this painstaking formalized form doesn't make the move any more or less T&E, even though the apparent increase in complexity may make it seem more like T&E to some people.

The other interesting thing is that, although Andrew and I (and possibly Afmob) essentially saw the same chain, it would be an absolute nightmare for Ruud or Richard (or anybody else) to build into their software. Not only are there neutral links in there, but several of the links in the chain are based on digit pairs, rather than single digits. Therefore, it's enlightening to see that something that humans can notice without much trouble requires an extremely elaborate and complicated implementation in order to be picked up by a future generation of automated solvers!

Andrew wrote:Mike's JSudoku analysis from his diagram is very interesting; I must admit I hadn't thought of looking at that particular relationship. It also works from the position after my step 22 except for the last line which doesn't yet apply. I wonder how much more work would be required to make that apply without resorting to the use of any chains.

I've updated my post above to provide more of JSudoku's steps, which should answer your question. No chains are required at all, anywhere along the line.

Andrew wrote:I'll rate A84V2 as 1.5 using the contradiction chain. I wonder what the rating would be without using it?

I would personally rate JSudoku's "no chain" solution path as "only" 1.75.

Andrew wrote:I wouldn't be surprised if SS rated it much higher since it will probably look at heavy combo crunching before trying any contradiction or forcing chain.

I know that SS can do the same moves as the ones performed by JSudoku, because I've seen it do them. Therefore, I'm wondering why the SScore is so high. From looking at the stats, SS also didn't use any chains or "45" moves labelled "insane", so I'm now asking myself where the very high rating came from...