4353:4353:4353:5124:4613:4613:4613:46163584
5124:5124:5124
4616:4616:4370:43702827:51243855
1305
5148:5148:5148:6943
259238753099
6943:6943:6943:5674
3875
23493366:6943:5674:5674
1844
5175:5175:5175:6202
261949263126:4673:6202:6202:6202
4926:4926
1608:4673:4673:62023141:3663
Guess I'll review my WT now before posting (if at all). BTW, I think it's slightly harder than the V1, so I would rate it as 1.5.I've now briefly compared my WT with Caida's. They are quite similar, so I won't provide a full WT, but instead just the following solving outline, simply to show how I got into the puzzle. Note that the key breakthrough move is step 7:I wrote:Guess I'll review my WT now before posting (if at all).
After solving the puzzle, I ran it through JSudoku, which didn't seem to have much trouble with it (compared to some V2s we've had in the past). Interested to see how it did it, I analyzed the log. Here's what I found out:Partial WT for Assassin 84V2
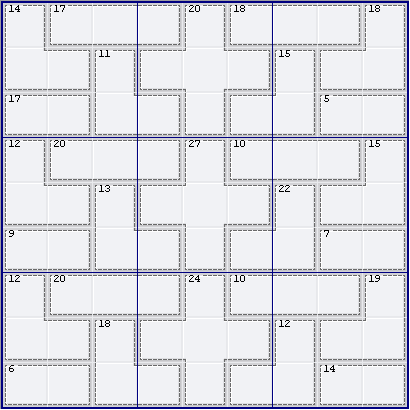
1. 17(2) at R3C12 = {89}, locked for R3 and N3
2. Outies N1: R13C4 = 14(2) = [86/95]
3. Outies N3: R13C6 = 11(2) = [47/74/83/92]
(Note: {56} combo blocked by R3C4)
4. R1C4 blocks {189} combo for 18(3) at R1C6
4a. -> no 1 in R1C78
5. {15689} unavailable in R3C6
5a. -> {159/168} combos blocked for 15(3) at R2C7
5a. -> no 1 in R23C7
6. Innies R1: R1C159 = 10(3)
6a. -> no 8,9
6b. -> 18(3) at R1C6 must have 1 of {89} ({567} blocked)
(Note: alternatively, {567} blocked by 17(3) at R1C2, which requires at least 1 of {567})
7. 18(3) at R1C9 cannot be {189}. Here's how:
7a. 18(3) at R1C9 = {189} forces {8/9} of 18(3) at R1C6 (step 6b) into R1C6
7b. -> R3C6 = {2/3} (step 3)
7c. but this eliminates all combinations for 5(2) at R3C8
7d. Conclusion: 18(3) at R1C9 <> {189}
7e. -> no 1 in 18(3) at R1C9
8. 1 of N3 now locked in R3C89 = {14}, locked for R3 and N3
The rest of the puzzle is fairly straightforward now (nothing worth writing home about).
The use of the chain in step 7 (although fairly quick to spot) was the reason for my rating of 1.5 for this puzzle.
Candidate diagram for JSudoku analysis above:The key move that JSudoku applied, which avoided the use of chains (but in exactly the same part of the grid as my chain in step 7) was based on the permutational analysis of the hidden innie/outie difference cage at R1C78+R3C6 (see step 4 below). From the candidate diagram shown, JSudoku progressed as follows:
1. 15(3) at R2C7 = {258/267/357/456} = {(5/6)..}
(Note: {348} blocked by 5(2) at R3C8; other combos blocked because both of {19} unavailable)
1a. {56} unavailable in R3C6
1b. -> R23C7 must contain at least 1 of {56}
2. 18(3) at R1C9 = {189/279/369/378/459/468} = {(8/9)..}
(Note: {567} blocked by R23C7 (step 1b))
3. Innies N3: R1C78+R23C7 = 22(4) = {2569/2578/3568/4567}
(Note: {2389} blocked by 18(3) (step 2); {2479/3469/3478} all blocked by 5(2) at R3C8; other combos blocked because 1 unavailable)
3a. 5 locked for N3
4. no 5 in R1C8. Here's how:
4a. I/O diff. N3: R1C78 = R3C6 + 7
4b. -> only possible permutations of R1C78+R3C6 with 5 in R1C8 are:
[452] - blocked by 5(2) at R3C8 = {(2/4)..}
[654] - blocked by R23C7 (step 1)
(Note: {56} blocked for R1C78 anyway, because 18(3) at R1C6 <> {567}, but JSudoku is clearly limiting its analysis to the cells belonging to the I/O diff. cage, and is not also pulling in R1C6 here)
4c. Conclusion: no 5 in R1C8
This locks the 5 of N3 into C7 (-> not elsewhere in C7), which makes a big difference.
Note: Step 4 is an advanced move that would be enough to justify a 1.5 rating on its own, IMHO.
Code: Select all
.-----------.-----------------------------------.-----------.-----------------------------------.-----------.
| 1234567 | 4567 12345 89 | 1234567 | 4789 2345678 23456789 | 1234567 |
| '-----------.-----------.-----------' '-----------.-----------.-----------' |
| 1234567 1234567 | 1234 | 12345678 123456789 123456789 | 235678 | 23456789 23456789 |
:-----------------------: '-----------. .-----------' :-----------------------:
| 89 89 | 1234 56 | 1234567 | 2347 234567 | 1234 1234 |
:-----------.-----------'-----------------------+-----------+-----------------------'-----------.-----------:
| 123456789 | 456789 3456789 345678 | 123456789 | 1234 1234567 1234567 | 12345678 |
| '-----------.-----------.-----------' '-----------.-----------.-----------' |
| 123456789 1234567 | 123456789 | 12345678 123456789 123456789 | 56789 | 12345678 12345678 |
:-----------------------: '-----------. .-----------' :-----------------------:
| 2345678 1234567 | 123456789 123456 | 123456789 | 5678 56789 | 123456 123456 |
:-----------.-----------'-----------------------+-----------+-----------------------'-----------.-----------:
| 123456789 | 456789 3456789 3456789 | 123456789 | 123467 1234567 1234567 | 23456789 |
| '-----------.-----------.-----------' '-----------.-----------.-----------' |
| 123456789 1234567 | 123456789 | 12345678 123456789 123456789 | 1234567 | 23456789 23456789 |
:-----------------------: '-----------. .-----------' :-----------------------:
| 1245 1245 | 123456789 2345678 | 123456789 | 346789 1234567 | 5689 5689 |
'-----------------------'-----------------------'-----------'-----------------------'-----------------------'
Prompted by that comment I tried to solve it without using a chain but gave up after step 22 where I had reached almost the same diagram as in Mike's 2nd message. I felt that my step 23 was a shortcut but maybe it doesn't count as a shortcut if one can't find any other way forward.Afmob wrote:Without using the forcing chain this assassin would have required lots of combo crunching.
Yes indeed, thanks Ruud! In particular, the difficulty of the puzzle was well-judged. Hard enough to require a bit of human ingenuity, yet not so hard that we were forced to resort to T&E.Andrew wrote:Thanks Ruud for a really challenging variant.
It's interesting to note that you found essentially the same chain as I did (step 7 of my partial WT). It's a perfectly valid chain in that none of the links depend on the side-effects (i.e., candidate/combo eliminations) of any preceding links, which is one of my main criteria for determining whether or not a chain is T&E. However, it's quite a complicated chain. If it were to be expressed in a formalized fashion, my step 7 would look something like this:Andrew wrote:I felt that my step 23 was a shortcut but maybe it doesn't count as a shortcut if one can't find any other way forward.
Select text in box (e.g., by triple-clicking it) to see what I wrote:(1)r3c89=(1,89)r1c9+r2c89-(8/9)r1c78=(8/9)r1c6,(2/3)r3c6-(23=1)r3c89
Note: I'm using the notation: "xy" => "x AND y", "x/y" => "x OR y" and "A,B" => "premise A => premise B (neutral link)". Note also that the chain begins with a strong link, as is the convention for AICs.
In other words:
7. Either r3c89 contains a 1, OR...
7a. r3c89 does not contain a 1
7b. -> r1c9+r2c89 must contain a 1 (strong link, N3)
7c. -> r1c9+r2c89 must also contain both 8 and 9 (neutral link, 18(3)n3)
7d. -> r1c78 cannot contain an 8 or 9 (weak link, N3)
7e. -> r1c6 must contain an 8 or 9 (strong link, 18(3)n23)
7f. -> r3c6 must contain a 2 or 3 (neutral link, h11(2)r13c6)
7g. -> r3c89 cannot contain both a 2 and a 3 (weak link, R3)
7h. -> r3c89 must contain a 1 (strong link, 5(2) cage)
7i. Conclusion: r3c89 must contain a 1
Suddenly, the chain looks a lot more complex! However, it's important to note that just because I often express chains in this painstaking formalized form doesn't make the move any more or less T&E, even though the apparent increase in complexity may make it seem more like T&E to some people.
The other interesting thing is that, although Andrew and I (and possibly Afmob) essentially saw the same chain, it would be an absolute nightmare for Ruud or Richard (or anybody else) to build into their software. Not only are there neutral links in there, but several of the links in the chain are based on digit pairs, rather than single digits. Therefore, it's enlightening to see that something that humans can notice without much trouble requires an extremely elaborate and complicated implementation in order to be picked up by a future generation of automated solvers!
I've updated my post above to provide more of JSudoku's steps, which should answer your question. No chains are required at all, anywhere along the line.Andrew wrote:Mike's JSudoku analysis from his diagram is very interesting; I must admit I hadn't thought of looking at that particular relationship. It also works from the position after my step 22 except for the last line which doesn't yet apply. I wonder how much more work would be required to make that apply without resorting to the use of any chains.
I would personally rate JSudoku's "no chain" solution path as "only" 1.75.Andrew wrote:I'll rate A84V2 as 1.5 using the contradiction chain. I wonder what the rating would be without using it?
I know that SS can do the same moves as the ones performed by JSudoku, because I've seen it do them. Therefore, I'm wondering why the SScore is so high. From looking at the stats, SS also didn't use any chains or "45" moves labelled "insane", so I'm now asking myself where the very high rating came from...Andrew wrote:I wouldn't be surprised if SS rated it much higher since it will probably look at heavy combo crunching before trying any contradiction or forcing chain.
